In the wake of the recent announcement from NASA’s Goddard Institute for Space Studies that global surface temperatures in February 2016 were an extraordinary 1.35 °C above the 1951-1980 baseline we bring you the third in our series of occasional guest posts.
Today’s article is a pre-publication draft prepared by Bill the Frog, who has also authorised me to reveal to the world the sordid truth that he is in actual fact the spawn of a “consumated experiment” conducted between Kermit the Frog and Miss Piggy many moons ago. Please ensure that you have a Microsoft Excel compatible spreadsheet close at hand, and then read on below the fold.
In a cleverly orchestrated move immaculately timed to coincide with the build up to the CoP21 talks in Paris, Christopher Monckton, the 3rd Viscount Monckton of Brenchley, announced the following startling news on the climate change denial site, Climate Depot …
Upon viewing Mr Monckton’s article, any attentive reader could be forgiven for having an overwhelming feeling of déjà vu. The sensation would be entirely understandable, as this was merely the latest missive in a long-standing series of such “revelations”, stretching back to at least December 2013. In fact, there has even been a recent happy addition to the family, as we learned in January 2016 that …
The primary eye-candy in Mr Monckton’s November article was undoubtedly the following diagram …
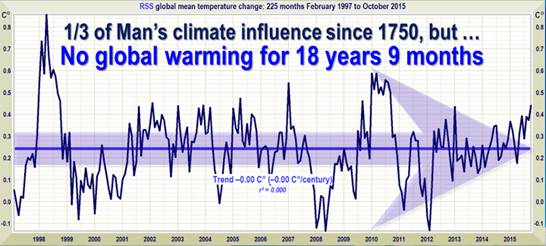
Fig 1: Copied from Nov 2015 article in Climate Depot
It is clear that Mr Monckton has the ability to keep churning out virtually identical articles, and this is a skill very reminiscent of the way a butcher can keep churning out virtually identical sausages. Whilst on the subject of sausages, the famous 19th Century Prussian statesman, Otto von Bismarck, once described legislative procedures in a memorably pithy fashion, namely that … “Laws are like sausages, it is better not to see them being made”.
One must suspect that those who are eager and willing to accept Mr Monckton’s arguments at face value are somehow suffused with a similar kind of “don’t need to know, don’t want to know” mentality. However, some of us are both able and willing to scratch a little way beneath the skin of the sausage. On examining one of Mr Monckton’s prize sausages, it takes all of about 2 seconds to work out what has been done, and about two minutes to reproduce it on a spreadsheet. That simple action is all that is needed to see how the appropriate start date for his “pause” automatically pops out of the data.
However, enough of the hors d’oeuvres, it’s time to see how those sausages get made. Let’s immediately get to the meat of the matter (pun intended) by demonstrating precisely how Mr Monckton arrives at his “no global warming since …” date. The technique is incredibly straightforward, and can be done by anyone with even rudimentary spreadsheet skills.
One basically uses the spreadsheet’s built-in features, such as the SLOPE function in Excel, to calculate the rate of change of monthly temperature over a selected time period. The appropriate command would initially be inserted on the same row as the first month of data, and it would set to range to the latest date available. This would be repeated (using a feature such as Auto Fill) on each subsequent row, down as far as the penultimate month. On each row, the start date therefore advances by one month, but the end date remains fixed. (As the SLOPE function is measuring rate of change, there must be at least two items in the range, that’s why the penultimate month would also be the latest possible start date.)
That might sound slightly complex, but if one then displays the results graphically, it becomes obvious what is happening, as shown below…
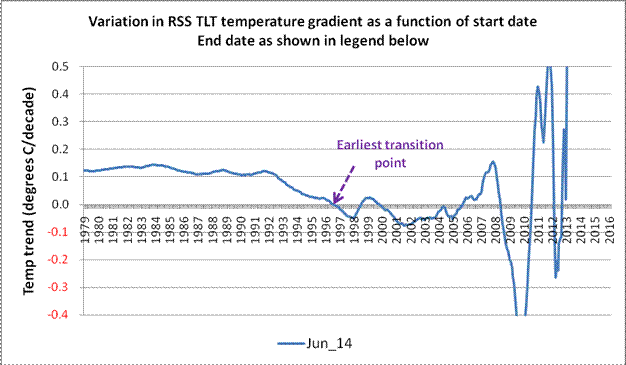
Fig 2: Variation in temperature gradient. End date June 2014
On the above chart (Fig 2), it can clearly be seen that, after about 13 or 14 years of stability, the rate of change of temperature starts to oscillate wildly as one looks further to the right. Mr Monckton’s approach has been simply to note the earliest transition point, and then declare that there has been no warming since that date. One could, if being generous, describe this as a somewhat naïve interpretation, although others may feel that a stronger adjective would be more appropriate. However, given his classical education, it is difficult to say why he does not seem to comprehend the difference between veracity and verisimilitude. (The latter being the situation when something merely has the appearance of being true – as opposed to actually being the real thing.)
Fig 2 is made up from 425 discrete gradient values, each generated (in this case) using Excel’s SLOPE function. Of these, 122 are indeed below the horizontal axis, and can therefore be viewed as demonstrating a negative (i.e. cooling) trend. However, that also means that 70% show a trend that is positive. Indeed, if one performs a simple arithmetic average across all 425 data points, the integration thus obtained is 0.148 degrees Celsius per decade.
(In the spirit of honesty and openness, it must of course be pointed out that the aggregated warming trend of 0.148 degrees Celsius/decade thus obtained has just about the same level of irrelevance as Mr Monckton’s “no warming since mm/yy” claim. Nether has any real physical meaning, as, once one gets closer to the end date(s), the values can swing wildly from one month to the next. In Fig 2, the sign of the temperature trend changes 8 times from 1996 onwards. A similar chart created at the time of his December 2013 article would have had no fewer than 13 sign changes over a similar period. This is because the period in question is too short for the warming signal to unequivocally emerge from the noise.)
As one adds more and more data, a family of curves gradually builds up, as shown in Fig 3a below.
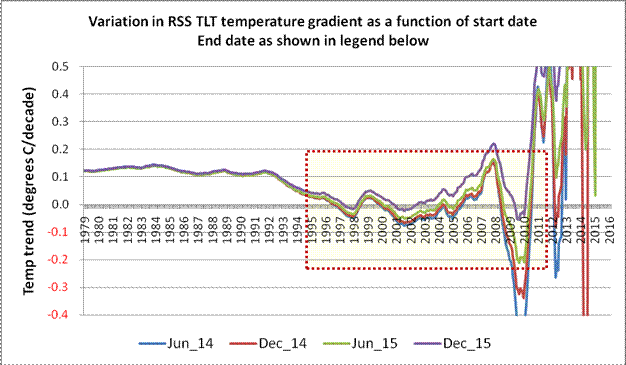
Fig 3a: Family of curves showing how end-date also affects temperature gradient
It should be clear from Fig 3a that each temperature gradient curve migrates upwards (i.e. more warming) as each additional 6-month block of data comes in. This is only to be expected, as the impact of isolated events – such as the temperature spike created by the 1997/98 El Niño – gradually wane as they get diluted by the addition of further data. The shaded area in Fig 3a is expanded below as Fig 3b in order to make this effect more obvious.

Fig 3b: Expanded view of curve family
By the time we are looking at an end date of December 2015, the relevant curve now consists of 443 discrete values, of which just 39, or 9%, are in negative territory. Even if one only considers values to the right of the initial transition point, a full 82% of these are positive. The quality of Mr Monckton’s prize-winning sausages is therefore revealed as being dubious in the extreme. (The curve has not been displayed, but the addition of a single extra month – January 2016 – further reduces the number of data points below the zero baseline to just 26, or 6%.) To anyone tracking this, there was only ever going to be one outcome, eventually, the curve was going to end up above the zero baseline. The ongoing El Niño conditions have merely served to hasten the inevitable.
With the release of the February 2016 data from RSS, this is precisely what happened. We can now add a fifth curve using the most up-to-date figures available at the time of writing. This is shown below as Fig 4.
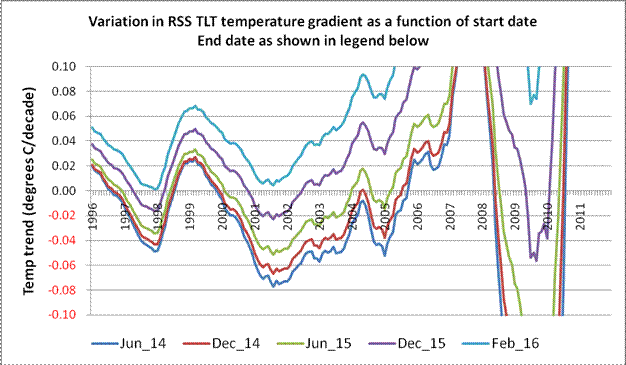
Fig 4: Further expansion of curve families incorporating latest available data (Feb 2016)
As soon as the latest (Feb 2016) data is added, the fifth member of the curve family (in Fig 4) no longer intersects the horizontal axis – anywhere. When this happens, all of Mr Monckton’s various sausages reach their collective expiry date, and his entire fantasy of “no global warming since mm/yy” simply evaporates into thin air.
Interestingly, although Mr Monckton chooses to restrict his “analysis” to only the Lower Troposphere Temperatures produced by Remote Sensing Systems (RSS), another TLT dataset is available from the University of Alabama in Huntsville (UAH). Now, this omission seems perplexing, as Mr Monckton took time to emphasise the reliability of the satellite record in his article dated May 2014.
In his Technical Note to this article, Mr Monckton tells us…
The satellite datasets are based on measurements made by the most accurate thermometers available – platinum resistance thermometers, which not only measure temperature at various altitudes above the Earth’s surface via microwave sounding units but also constantly calibrate themselves by measuring via spaceward mirrors the known temperature of the cosmic background radiation, which is 1% of the freezing point of water, or just 2.73 degrees above absolute zero. It was by measuring minuscule variations in the cosmic background radiation that the NASA anisotropy probe determined the age of the Universe: 13.82 billion years.
Now, that certainly makes it all sound very easy. It’s roughly the metaphorical equivalent of the entire planet being told to drop its trousers and bend over, as the largest nurse imaginable approaches, all the while gleefully clutching at a shiny platinum rectal thermometer. Perhaps a more balanced perspective can be gleaned by reading what RSS themselves have to say about the difficulties involved in Brightness Temperature measurement.
When one looks at Mr Monckton’s opening sentence referring to “the most accurate thermometers available”, one would certainly be forgiven for thinking that there must perforce be excellent agreement between the RSS and UAH datasets. This meme, that the trends displayed by the RSS and UAH datasets are in excellent agreement, is one that appears to be very pervasive amongst those who regard themselves as climate change sceptics. Sadly, few of these self-styled sceptics seem to understand the meaning behind the motto “Nullius in verba”.
Tellingly, this “RSS and UAH are in close agreement” meme is in stark contrast to the views of the people who actually do that work for a living.
Carl Mears (of RSS) wrote an article back in September 2014 discussing the reality – or otherwise – of the so-called “Pause”. In the section of this article dealing with measurement errors, he wrote that …
A similar, but stronger case can be made using surface temperature datasets, which I consider to be more reliable than satellite datasets (they certainly agree with each other better than the various satellite datasets do!) [my emphasis]
The views of Roy Spencer from UAH concerning the agreement (or, more accurately, the disagreement) between the two satellite datasets must also be considered. Way back in July 2011, Dr Spencer wrote …
… my UAH cohort and boss John Christy, who does the detailed matching between satellites, is pretty convinced that the RSS data is undergoing spurious cooling because RSS is still using the old NOAA-15 satellite which has a decaying orbit, to which they are then applying a diurnal cycle drift correction based upon a climate model, which does not quite match reality.
So there we are, Carl Mears and Roy Spencer, who both work independently on satellite data, have views that are somewhat at odds with those of Mr Monckton when it comes to agreement between the satellite datasets. Who do we think is likely to know best?
The closing sentence in that paragraph from the Technical Note did give rise to a wry smile. I’m not sure what relevance Mr Monckton thinks there is between global warming and a refined value for the Hubble Constant, but, for whatever reason, he sees fit to mention that the Universe was born nearly 14 billion years ago. The irony of Mr Monckton mentioning this in an article which treats his target audience as though they were born yesterday appears to have passed him by entirely.
Moving further into Mr Monckton’s Technical Note, the next two paragraphs basically sound like a used car salesman describing the virtues of the rust bucket on the forecourt. Instead of trying to make himself sound clever, Mr Monckton could simply have said something along the lines of … “If you want to verify this for yourself, it can easily be done by simply using the SLOPE function in Excel”. Of course, Mr Monckton might prefer his readers not to think for themselves.
The final paragraph in the Technical Note reads as follows…
Dr Stephen Farish, Professor of Epidemiological Statistics at the University of Melbourne, kindly verified the reliability of the algorithm that determines the trend on the graph and the correlation coefficient, which is very low because the data are highly variable and the trend is flat.
Well, this is an example of the logical fallacy known as “Argument from Authority” combined with a blatant attempt at misdirection. The accuracy of the “… algorithm that determines the trend …” has absolutely nothing to do with Mr Monckton’s subsequent interpretation of the results, although that is precisely what the reader is meant to think. The good professor may well be seriously gifted at statistics, but that doesn’t mean he speaks with any authority about atmospheric science or about satellite datasets.
Also, for the sake of the students at Melbourne University, I would hope that Mr Monckton was extemporizing at the end of that paragraph. It is simply nonsense to suggest that the “flatness” of the trend displayed in his Fig 1 is in any way responsible for the trend equation also having an R2 value of (virtually) zero. The value of the coefficient of determination (R2) ranges from 0 to 1, and wildly variable data can most certainly result in having a value of zero, or thereabouts, but the value of the trend itself has little or no bearing upon this.
The phraseology used in the Technical Note would appear to imply that, as both the trend and the coefficient of determination are effectively zero, this should be interpreted as two distinct and independent factors which serve to corroborate each other. Actually, nothing could be further from the truth.
The very fact that the coefficient of determination is effectively zero should be regarded as a great big blazing neon sign which says “the equation to which this R2 value relates should be treated with ENORMOUS caution, as the underlying data is too variable to infer any firm conclusions”.
To demonstrate that a (virtually) flat trend can have an R2 value of 1, anyone can try inputting the following numbers into a spreadsheet …
10.0 10.00001 10.00002 10.00003 etc.
Use the Auto Fill capability to do this automatically for about 20 values. The slope of this set of numbers is a mere one part in a million, and is therefore, to all intents and purposes, almost perfectly is flat. However, if one adds a trend line and asks for the R2 value, it will return a value of 1 (or very, very close to 1). (NB When I tried this first with a single recurring integer – i.e. absolutely flat – Excel returned an error value. That’s why I suggest using a tiny increment, such as the 1 in a million slope mentioned above.)
Enough of the Technical Note nonsense, let’s looks at the UAH dataset as well. Fig 5 (below) is a rework of the earlier Fig 2, but this time with the UAH dataset added, as well as an equally weighted (RSS+UAH) composite.
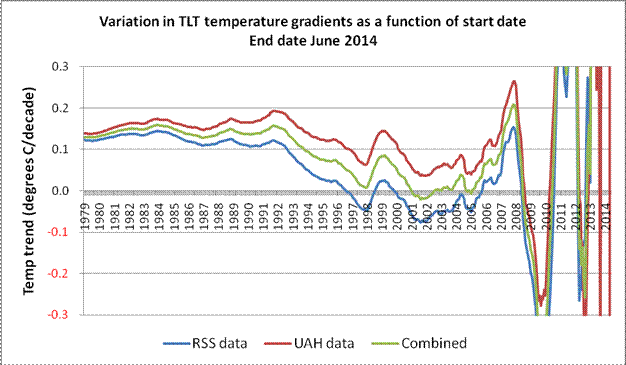
Fig 5: Comparison between RSS and UAH (June 2014)
The difference between the RSS and UAH results makes it clear why Mr Monckton chose to focus solely on the RSS data. At the time of writing this present article, the RSS and UAH datasets each extended to February 2016, and Fig 6 (below) shows graphically how the datasets compare when that end date is employed.
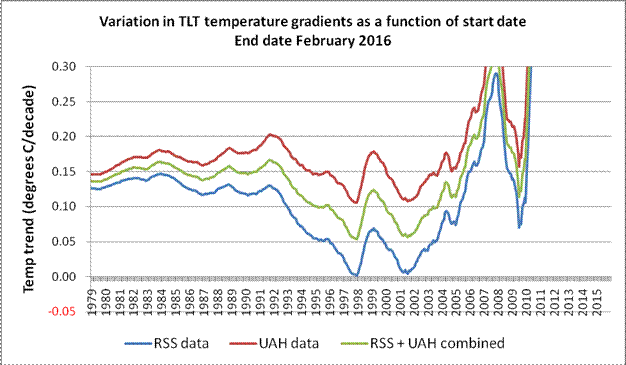
Fig 6: Comparison between RSS and UAH (Feb 2016)
In his sausage with the November 2015 sell-by-date, Mr Monckton assured his readers that “…The UAH dataset shows a Pause almost as long as the RSS dataset.“
Even just a moment or two spent considering the UAH curves on Fig 5 (June 2014) and then on Fig 6 (February 2016) would suggest precisely how far that claim is removed from reality. However, for those unwilling to put in this minimal effort, Fig 7 is just for you.

Fig 7: UAH TLT temperatures gradients over three different end dates.
From the above diagram, it is rather difficult to see any remote justification for Mr Monckton’s bizarre assertion that “…The UAH dataset shows a Pause almost as long as the RSS dataset.“
Moving on, it is clear that, irrespective of the exact timeframe, both the datasets exhibit a reasonably consistent “triple dip”. To understand the cause(s) of this “triple dip” in the above diagrams (at about 1997, 2001 and 2009), one needs to look at the data in the usual anomaly format, rather than in gradient format used in Figs 2 – 7.
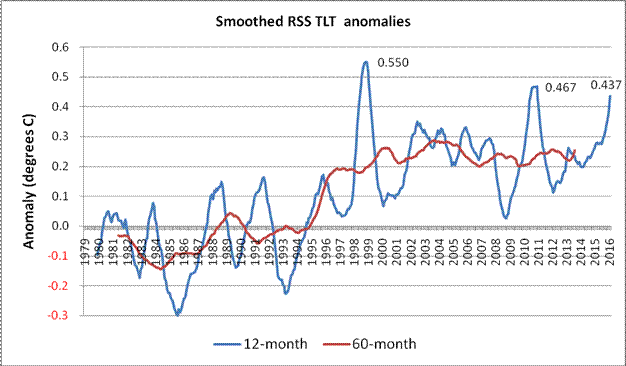
Fig 8: RSS TLT anomalies smoothed over 12-month and 60-month periods
The monthly data looks very messy on a chart, but the application of 12-month and 60-month smoothing used in Fig 8 perhaps makes some details easier to see. The peaks resulting from the big 1997/98 El Niño and the less extreme 2009/10 event are very obvious on the 12-month data, but the impact of the prolonged series of 4 mini-peaks centred around 2003/04 shows up more on the 60-month plot. At present, the highest 60-month rolling average is centred near this part of the time series. (However, that may not be the case for much longer. If the next few months follow a similar pattern to the 1997/98 event, both the 12- and 60-month records are likely to be surpassed. Given that the March and April RSS TLT values recorded in 2015 were the two coolest months of that year, it is highly likely that a new rolling 12-month record will be set in April 2016.)
Whilst this helps explain the general shape of the curve families, it does not explain the divergence between the RSS and the UAH data. To show this effect, two approaches can be adopted: one can plot the two datasets together on the same chart, or one can derive the differences between RSS and UAH for every monthly value and plot that result.
In the first instance, the equivalent UAH rolling 12- and 60-month values have effectively been added to the above chart (Fig 8), as shown below in Fig 9.
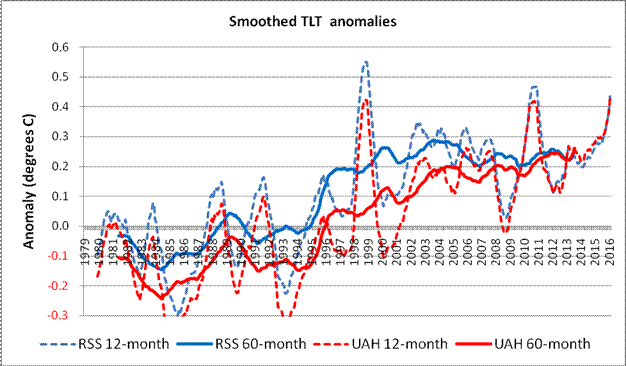
Fig 9: RSS and UAH TLT anomalies using 12- and 60-month smoothing
On this chart (Fig 9) it can be seen that the smoothed anomalies start a little way apart, diverge near the middle of the time series, and then gradually converge as one looks toward the more recent values. Interestingly, although the 60-month peak at about 2003/04 in the RSS data is also present in the UAH data, it has long since been overtaken.
The second approach would involve subtracting the UAH monthly TLT anomalies figures from the RSS equivalents. The resulting difference values are plotted on Fig 10 below, and are most revealing. The latest values on Figs 9 and 10 are for February 2016.
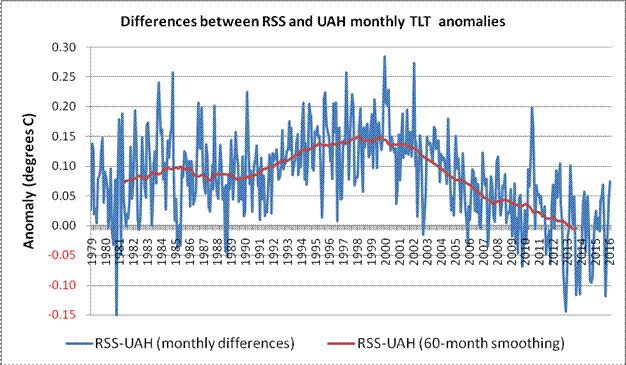
Fig 10: Differences between RSS and UAH monthly TLT values up to Feb 2016
Even without the centred 60-month smoothed average, the general shape emerges clearly. The smoothed RSS values start off about 0.075 Celsius above the UAH values, but by about 1999 or 2000, this delta has risen to +0.15 Celsius. It then begins a virtually monotonic drop such that the 6 most recent rolling 60-month values have gone negative.
NB It is only to be expected that the dataset comparison begins with an offset of this magnitude. The UAH dataset anomalies are based upon a 30-year meteorology stretching from 1981 – 2010. However, RSS uses instead a 20-year baseline running from 1979 – 1998. The mid points of the two baselines are therefore 7 years apart. Given that the overall trend is currently in the order of 0.12 Celsius per decade, one would reasonably expect the starting offset to be pretty close to 0.084 Celsius. The actual starting point (0.075 Celsius) was therefore within about one hundredth of a degree Celsius from this figure.
Should anyone doubt the veracity of the above diagram, hereis a copy of something similar taken from Roy Spencer’s web pages. Apart from the end date, the only real difference is that whereas Fig 9 has the UAH monthly values subtracted from the RSS equivalent, Dr Spencer has subtracted the RSS data from the UAH equivalent, and has applied a 3-month smoothing filter. This is reproduced below as Fig 11.
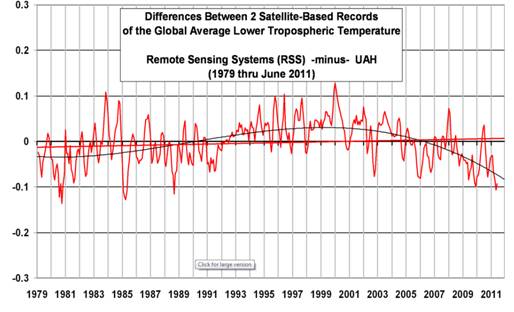
Fig 11: Differences between UAH and RSS (copied from Dr Spencer’s blog)
This actually demonstrates one of the benefits of genuine scepticism. Until I created the plot on Fig 10, I was sure that the 97/98 El Niño was almost entirely responsible for the apparent “pause” in the RSS data. However, it would appear that the varying divergence from the equivalent UAH figures also has a very significant role to play. Hopefully, the teams from RSS and UAH will, in the near future, be able to offer some mutually agreed explanation for this divergent behaviour. (Although both teams are about to implement new analysis routines – RSS going From Ver 3.3 to Ver 4, and UAH going from Ver 5.6 to Ver 4.0 – mutual agreement appears to be still in the future.)
Irrespective of this divergence between the satellite datasets, the October 2015 TLT value given by RSS was the second largest in that dataset for that month. That was swiftly followed by monthly records for November, December and January. The February value went that little bit further and was the highest in the entire dataset. In the UAH TLT dataset, September 2015 was the third highest for that month, with each of the 5 months since then breaking the relevant monthly record. As with its RSS equivalent, the February 2016 UAH TLT figure was the highest in the entire dataset. In fact, the latest rolling 12-month UAH TLT figure is already the highest in the entire dataset. This would certainly appear to be strange behaviour during a so-called pause.
As sure as the sun rises in the east, these record breaking temperatures (and their effect on temperature trends) will be written off by some as merely being a consequence of the current El Niño. It does seem hypocritical that these people didn’t feel that a similar argument could be made about the 1997/98 event. An analogy could be made concerning the measurement of Sea Level Rise. Imagine that someone – who rejects the idea that sea level is rising – starts their measurements using a high tide value, and then cries foul because a subsequent (higher) reading was also taken at high tide.
This desperate clutching of straws will doubtless continue unabated, and a new “last, best hope” has already appeared in guise of Solar Cycle 25. Way back in 2006, an article by David Archibald appeared in Energy & Environment telling us how Solar Cycles 24 & 25 were going to cause temperatures to plummet. In the Conclusion to this paper, Mr Archibald wrote that …
A number of solar cycle prediction models are forecasting weak solar cycles 24 and 25 equating to a Dalton Minimum, and possibly the beginning of a prolonged period of weak activity equating to a Maunder Minimum. In the former case, a temperature decline of the order of 1.5°C can be expected based on the temperature response to solar cycles 5 and 6.
Well, according to NASA, the peak for Solar Cycle 24 passed almost 2 years ago, so it’s not looking too good at the moment for that prediction. However, Solar Cycle 25 probably won’t peak until about 2025, so that will keep the merchants of doubt going for a while.
Meanwhile, back in the real world, it is very tempting to make the following observations …
- The February TLT value from RSS seems to have produced the conditions under which certain allotropes of the fabled element known as Moncktonite will spontaneously evaporate, and …
- If Mr Monckton’s sausages leave an awfully bad taste in the mouth, it could be due to the fact that they are full of tripe.
Inevitably however, in the world of science at least, those who seek to employ misdirection and disinformation as a means to further their own ideological ends are doomed to eventual failure. In the closing paragraph to his “Personal
observations on the reliability of the Shuttle”, the late, great Richard Feynman used a phrase that should be seared into the consciousness of anyone writing about climate science, especially those who are economical with the truth…
For a successful technology, reality must take precedence over public relations, for nature cannot be fooled.
Remember that final phrase – “nature cannot be fooled”, even if vast numbers of voters can be!
@Bill_The_Frog has only been on Twitter for one day, but already lots of people are chattering about him and his draft paper.
One of them is Christopher Monckton, the 3rd Viscount Monckton of Brenchley!
We have offered Mr. Monckton the opportunity to reply publicly to the points raised by Bill The Frog’s article, but he has declined.
Personally I don’t have much hope for a productive exchange given the tone adopted by Patrick Moore and the Clerk to His Lordship :
Lovely. I treasure this antique which demonstrates that the more things change the more they stay the same. You might also be interested in a teensy bit of Jane Mayer’s Dark Money that I banged out and posted on aTTP’s penultimate article.
http://duoquartuncia.blogspot.com/2008/07/aps-and-global-warming-what-were-they.html
As you can see in the comment section therein, arguers never give up. They’re not interested in anything but making a big noise and sounding too pompous to disbelieve.
Thanks for that blast from the past Susan. Plus ça change, n’est-ce pas? For those that are not au fait with the “aTTP” reference, please see Susan’s comment at:
Should we conclude from all this that now would be a good time to declare to the world that Bill’s magnum opus is in actual fact a “major PEER-REVIEWED scientific paper mathematically disproving the pause in AGW in a GWC JOURNAL”. You and I both approve of it after all, and we are undoubtedly Bill’s peers (with a small p)!